[4점공략] 2020 6월 고3 평가원 모의고사 수학 가형 30번

​

2020학년도 6월 고3 평가원 모의고사 수학 가형 30번 문제입니다.

​

출제영역은 미적분 영역입니다.

이 문제는 아래에 제시해준 \( f \)의 그래프라든가

​

수열 \( c_n \)의 정의된 모양을 살펴보면 굉장히 복잡해보이지만,

​

문제 내에 힌트가 많이 주어지고 있으며, 힌트에 대해서 조금만 생각해보면

​

크게 어려운 문제는 아니었습니다.

​

실제로 30번 문제의 오답률은 93% 정도로(EBSi 기준), 다른 모의고사 수학 가형의 30번에 비해서

​

오답률이 높지 않습니다(물론 93%라는 수치 자체는 엄청 높은 수치임은 확실합니다만..)

​

​

그럼 어떤 식으로 문제에서 힌트를 주고 있고, 어떤 식으로 이용해서 풀 수 있는지 한번 살펴보겠습니다.

​

​

문제를 읽어보겠습니다.

 

상수 \( a \), \( b \)에 대하여 함수 \( f(x) = a \sin ^3 x + b \cos x \)가

$$ f\left(\frac{\pi}{4}\right)=3\sqrt{2}, \ f\left(\frac{\pi}{3}\right)=5\sqrt{3} $$

을 만족

 

함수 \( f \)가 주어져 있고, 함수식 내에는 두 개의 값이 알려지지 않은 상수가 있으며,

​

함숫값을 두 개 알려주고 있습니다.

​

각각의 함숫값을 이용하여 두 일차식을 만들어낸 후 \( a \), \( b \)의 값을 알아낼 수 있는데,

​

단지 연립일차방정식을 풀 수 있는지만을 물어보려고 일부러 \( a \), \( b \)를 둔 다음

​

두 함숫값을 준 것은 아닐 것입니다.

​

하지만 아직은 이렇게 문제를 구성한 진정한 이유를 알 수 없으니

​

일단 당장 해결할 수 있는 연립일차방정식부터 풀어봅시다.

$$ \begin{cases} a \cdot \frac{2\sqrt{2}}{8} + b \cdot \frac{\sqrt{2}}{2} = 3\sqrt{2} \\ a \cdot \frac{3\sqrt{3}}{8} + b \cdot \frac{\sqrt{3}}{2} = 5\sqrt{3} \end{cases} $$

 

여기까지 해 두고 문제의 다음 부분을 읽어보겠습니다.

 

실수 \( t(1<t<14) \)에 대하여 함수 \( y=f(x) \)의 그래프와 직선 \( y=t \)가 만나는 점의 \( x \)좌표 중 양수인 것을 작은 수부터 순서대로 나열한 것을 \( x_n \)

 

\( x_n \)에 대한 정의가 나오고 있습니다.

​

문제 다음 부분에 나오는 수열 \( c_n \)은 이 \( x_n \)을 이용한 식이기 때문에,

​

\( x_n \)에 대해서 짚고 넘어갈 필요가 있습니다.

​

우선 \( t \)라는 새로운 변수가 등장하는데, \( t \)의 범위는 \( 1<t<14 \)로 주어져 있습니다.

​

직선 \( y=t \)는 \( y=f(x) \)의 그래프 위에서 \( t \)의 값에 따라 움직이는 수평선인데,

​

이 \( t \)의 값이 제한되었다는 것은 \( t \)의 값이 \( f(x) \)의 특정 함숫값을 초과하거나 미만이 되지 않도록 하여

​

\( x_n \)의 개수 또는 나타나는 위치가 변동되지 않도록 하는 것으로 보입니다.

​

일단 \( 14 \)라는 특별한 수는 \( f(x) \)의 식으로 볼 때 \( f(x) \)의 최댓값인 듯한데,

​

짐작만으로는 정확하게 알아낼 수 없으니 미분을 통하여 그래프 및 함숫값의 위치를 알아보도록 합시다.

​

(그래프가 주어져있긴 하지만, 단순히 곡선만 있을 뿐이지

\( x \)가 몇일 때 최댓값인지, 함숫값이 몇인지 이런 정보는 없기 때문에 조사해볼 필요가 있습니다)

 

$$ f'(x) = 48 \sin ^2 x \cos x - 2 \cos x \\ \qquad = 2 \cos x \left( 24 \sin ^2 x - 1 \right) $$

 

여기서

$$ \cos x = 0 \ 또 는 \ \sin x = \pm \frac{1}{2\sqrt{6}} $$

이 되도록 하는 \( x \)값에서 극값을 가짐을 알 수 있습니다.

$$ \cos x = 0 $$

이 되도록 하는 \( x \)의 값은

$$ x = \frac{\pi}{2}, \ \frac{3}{2}\pi, \ \frac{5}{2}\pi, \ \cdots $$

와 같은 값들일 것이고,

(양수인 부분만 생각하는 것으로 합니다)

 

$$ \sin x = \pm \frac{1}{2\sqrt{6}} $$

이 되도록 하는 \( x \)의 값은 정확히 구하기 어렵지만, 각각

 

$$ 0<x<\frac{\pi}{2}, \ \frac{\pi}{2}<x<\pi, \ \pi<x<\frac{3}{2}\pi, \\ \cdots $$

사이에 있는 어떤 값들로 이해할 수 있습니다.

​

어디에서 극대인지, 극소인지를 알아내려면 문제에서 그래프가 주어지지 않았다면 구해야 하겠지만,

​

그래프가 주어졌기 때문에 극값을 갖는 \( x \)값들을 작은 것부터 나열하는 것만으로도 충분합니다.

​

이를 그래프상에 표시하면 <그림 1>과 같습니다.

​

​

<그림 1>

​

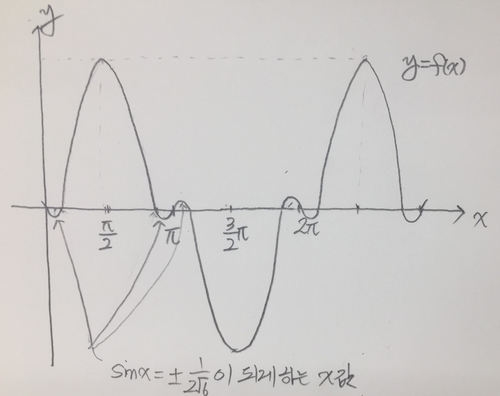
또한, 극점에서의 함숫값을 알아보기 위해 극값을 \( f \)에 대입해봅니다.

​

$$ x = \frac{\pi}{2} \ 일 \ 때, \ f(x)=14, $$

$$ \sin x = \frac{1}{2\sqrt{6}} \ 일 \ 때, $$

$$ f(x)=16\cdot \frac{1}{48\sqrt{6}} - 2\cdot \frac{1}{2\sqrt{6}} \\ \qquad=-\frac{2}{3\sqrt{6}}=-\frac{\sqrt{6}}{9} $$

 

\( f \)가 주기함수 및 대칭구조를 이루고 있기 때문에 어느 하나에서의 함숫값을 구하는 것만으로도

​

다른 함숫값들을 알아낼 수 있으므로, 경우별로 하나씩만 조사하였습니다.

​

주어진 함수의 최댓값은 \( 14 \)이고,

​

\( \sin x = \pm \frac {1}{2\sqrt{6}} \) 일때의 함숫값들의 절댓값은 \( 1 \)보다 작습니다.

​

이상의 상황 및 \( y=t \) 그래프와 그에 따른 \( x_n \)들을 그래프상에 표시하면

​

<그림 2>와 같습니다.

​

<그림 2>

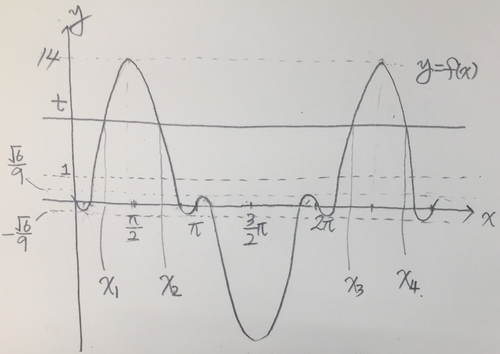
이를 통해서, \( 1<t<14 \) 라는 \( t \)의 범위는 \( x_n \)들이 특정한 위치에서만

​

나타나도록 제한된 것이라는 것을 알 수 있습니다.

​

물론 정확히 \( \frac{\sqrt{6}}{9} < t < 14 \) 라고 주지는 않았지만,

​

문제의 간결성을 위해서 또는 구체적인 수치를 최대한 숨기기 위해서

​

적당히 \( 1 \)로 놓은 것으로 보입니다.

​

\( x_n \)에 대한 분석이 끝났으므로 문제의 다음 부분을 읽어보겠습니다.

 

$$ c_n = \int_{3\sqrt{2}}^{5\sqrt{3}} \frac{t}{f'(x_n)} \, dt $$

 

\( c_n \)에 대한 정의가 정적분으로 주어져 있는데,

​

여기서 아래끝과 위끝을 보면 문제의 처음 부분에서 보았던 숫자가 보입니다.

​

\( 3\sqrt{2} \), \( 5\sqrt{3} \)이라는 값은 특정 \( x \)값에 대한 \( f \)의 함숫값들인데,

​

이들이 아래끝과 위끝으로 등장했다는 것은, \( f \)의 역함수에 대한 적분을 떠올리게 합니다.

​

즉, 앞에서 단순히 일차연립방정식을 물어보려고 함숫값들을 준 것이 아니라,

​

이런 점을 쉽게 파악할 수 있도록 하는 힌트를 주기 위해서 그렇게 준 것이었습니다.

​

따라서 이 정적분을 계산할 때는 \( f \)의 역함수를 이용해야 한다는 점을 염두에 두어야 합니다.

​

​

그런데 \( f \)는 기본적으로 일대일함수가 아니기 때문에 역함수가 존재하는 함수는 아닙니다.

​

하지만 \( f \)의 정의역을 제한하여 순증가함수 또는 순감소함수를 만들어낼 수 있다면

​

그러한 함수의 역함수를 생각해볼 수는 있습니다.

​

예를 들어, \( f \)의 정의역을 <그림 3>과 같이 제한해보겠습니다.

​

<그림 3>

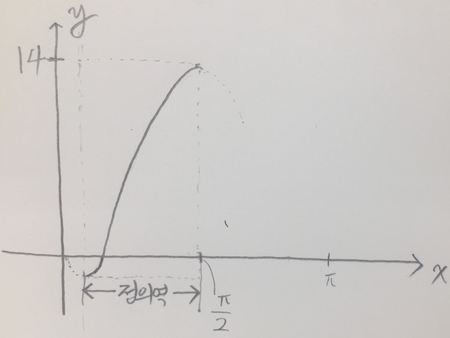
이렇게 정의역을 제한하여 만든 순증가함수의 역함수는 생각해볼 수 있는 것입니다.

​

여기서 \( y=t \) 라는 직선을 추가하여 생각해보겠습니다.

​

<그림 4>

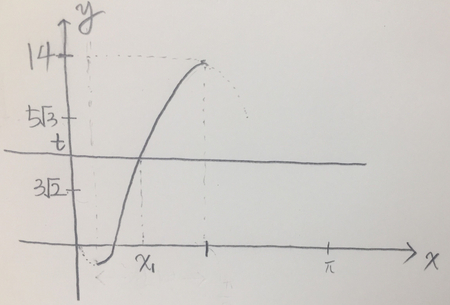
<그림 4>에서 알 수 있듯이, <그림 3>에서 제한한 정의역에 포함되는 \( x_n \)의 값들은 \( x_1 \) 뿐입니다.

​

그래서 이렇게 정의역을 제한한 함수에서는 \( c_1 \)의 값만을 생각해볼 수밖에 없을 듯합니다.

$$ c_1 = \int_{3\sqrt{2}}^{5\sqrt{3}} \frac{t}{f'(x_1)} \, dt $$

이때 그래프상에서,

$$ x_1 = f^{-1}(t) $$

임을 알 수 있으므로,

( ※ f의 정의역을 제한한 새로운 함수는 f와 다른 함수입니다.

수식은 같지만 정의역이 다르기 때문입니다.

따라서 정의역을 제한한 새로운 함수를 다시 f로 부르는 것은 문제가 있고,

새로운 함수를 표현하기 위해서 f에 첨자를 붙여서 사용하거나 다른 표현을 사용해야 하지만,

본 문제에서는 풀이의 간결성을 위해서 정의역을 제한한 함수를 다시 f로 부르겠습니다.)

​

\( c_1 \)의 계산식을 다음과 같이 다시 쓸 수 있습니다.

$$ c_1 = \int_{3\sqrt{2}}^{5\sqrt{3}} \frac{t}{f'(f^{-1}(t))} \, dt $$

여기서

$$ f^{-1}(t)=k $$

로 치환하면,

$$ \frac{1}{f'(f^{-1}(t))}dt=dk $$

이고, 이들을 이용하여 정적분 식을 다시 쓰면

$$ c_1 = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} t \, dk $$

가 되는데,

$$ f^{-1}(t)=k \ \rightarrow \ t=f(k) $$

이므로,

$$ c_1 = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} f(k) \, dk = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} f(x) \, dx $$

가 되어 결국 구하는 것은

​

<그림 5>

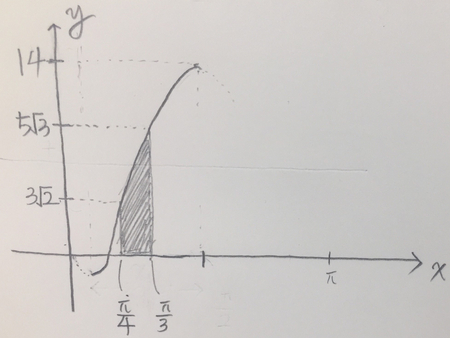
<그림 5>에 어둡게 표시된 면적입니다.

​

계산해봅시다.

 

$$ \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \left( 16\sin ^3 x - 2 \sin x \right) \, dx $$

$$ = 16 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin ^ 3 x \, dx - 2 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin x \, dx $$

$$ 16 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin ^ 3 x \, dx \ 를 \ 먼 저 \ 계 산 하 면, $$

$$ 16 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin ^ 3 x \, dx \\ = 16 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin x \left(1- \cos ^2 x \right) \, dx. $$

$$ \cos x = t \ 라 \ 하 면, -\sin x dx = dt. $$

$$ \therefore \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin ^ 3 x \, dx = 16 \int_{\frac{1}{2}}^{\frac{\sqrt{2}}{2}} \left( t^2 - 1 \right) \, dt \\ = 16 \left[ \frac{1}{3} t^3 - 1 \right] _{\frac{\sqrt{2}}{2}}^{\frac{1}{2}} $$

$$ =- \frac{22}{3} + \frac{20}{3} \sqrt{2}. $$

$$ 2 \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \sin x dx = -1+\sqrt{2} \ 이 므 로 $$

$$ ( 준 식 ) = - \frac{19}{3} + \frac{17}{3} \sqrt{2} = c_1. $$ 

 

이때 \( f \) (원래의 \( f \))는 주기가 \( 2π \)인 함수이므로,

​

<그림 2>에서 표시했던 \( x_n \) 값들의 위치로 보았을 때,

 

\( c_1 = c_3 = c_5 = \cdots \)

 

가 성립함을 알 수 있습니다.

​

홀수인 \( n \)에 대해 각 \( x_n \)이 포함되는 정의역으로 제한한 순증가함수를 생각하였을 때,

​

각 \( c_n \)별로 똑같은 면적을 계산하게 되기 때문입니다.

​

​

그렇다면 짝수인 \( n \)에 대해서는 어떨까요?

​

<그림 6>

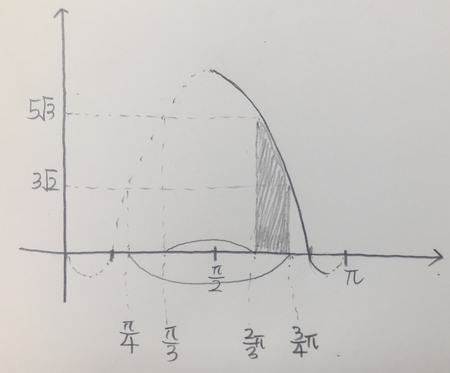
이번엔 \( x_2 \)가 포함되는, 순감소부분만을 정의역으로 취한 \( f \)의 한 부분을 설정하였습니다.

​

이 경우,

 

$$ c_2 = \int_{3\sqrt{2}}^{5\sqrt{3}} \frac{t}{f'(f^{-1}(t))} \, dt $$

 

에서 c_1의 경우와 같이 치환적분법을 이용하면

 

$$ c_2 = \int_{\frac{3}{4}\pi}^{\frac{2}{3}\pi}f(x) \, dx = -\int_{\frac{2}{3}\pi}^{\frac{3}{4}\pi} f(x) \, dx $$

 

가 됩니다. <그림 6>에 표시한 면적의 값에 마이너스가 붙는 꼴인데,

​

<그림 6>에 표시한 면적은 대칭성에 의해 <그림 5>에 표시한 면적과 같습니다.

​

따라서,

 

$$ c_2 = -c_1 $$

 

이 되며, 이는 다른 짝수 \( n \)에 대해서도 그러하므로

​

\( c_1 \) 부터 \( c_{100} \) 까지를 모두 더하면 \( 0 \)이 됩니다.

​

결국은 구하는 값

 

$$ \sum_{n=1}^{101} c_n = c_{101} = -\frac{19}{3} + \frac{17}{3} \sqrt{2} $$

 

가 됩니다.

​

따라서

$$ p = - \frac{19}{3}, \ q = \frac{17}{3}, \\ q-p=12 $$

가 되어 최종적인 정답은 12가 됩니다.

​

​

\( c_n \)도 이상하게 생겼고, 그래프도 복잡해보여서 선뜻 접근하기 어려워보이는 문제이지만,

​

그런 문제일 수록 출제자가 주는 힌트가 문제 속에 있으며,

​

그걸 잘 파악하는 것이 문제 해결의 핵심적인 열쇠가 됩니다.

​

물론 그런 걸 잘 파악하는 것도 평소에 문제를 푸는 수많은 연습이 동반되어야 가능한 것일 겁니다.

​

​

​

이상으로 2020학년도 6월 고3 평가원 모의고사 수학 가형 30번 문제 풀이를 마치겠습니다.

 

 

 

대학 입시 고민, 모르는 과학 문제, 서울대학교 사범대 출신 선생님의 풍부한 공/사교육 경험으로 해결해드립니다. (현재 무료!)

'포랩(PoLAB)' - 입시 질문, 과학 공부 질문, 여기에 물어보세요!