| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 고등학생
- 수학가형21번
- 바른생수
- 생명과학
- 1등급사과
- customdialog
- xcode
- kotlin
- MNIST
- Unity
- 내신
- ios
- Firebase
- 플레이스토어
- 유니티
- 개발일지
- 개발
- JavaScript
- 과탐
- LineRenderer
- 수능
- 모의고사
- PoLAB
- 포랩
- 수학가형
- 딥러닝
- 코틀린
- 생명과학1
- Android
- 고등학교
- Today
- Total
수학적 접근
[4점공략] 2020 6월 고3 평가원 모의고사 수학 가형 29번 본문

2020학년도 6월 고3 평가원 모의고사 수학 가형 30번 문제입니다.
출제 영역은 기하와 벡터입니다.
29번 문제의 오답률은 92.4% (EBSi 기준) 정도로 30번 문제(92.9%) 와
오답률의 차이가 거의 없었습니다.
이번 29번 문제가 여태껏 출제되었던 다른 시험의 29번 벡터 문항들과 비교해서
크게 어려운 문제는 아니었는데, 6월 모평에서는 아직 기하와 벡터 과목의
전 영역이 출제되지 않기 때문에, 수험생들이 벡터에 익숙하지 않아서 그런 것으로 생각됩니다.
또한 문제가 길어서 문제를 분석하는 데 충분한 시간을 갖지 못했을 수도 있었을 듯합니다.
그럼 문제를 차근차근 읽어보면서 풀어가보겠습니다.
좌표평면에서 \( C: y=\sqrt{8 - x^2} (2 \le x \le 2\sqrt{2}) \) 위의 점 \( \textrm{P} \)에 대하여
\( \overline{OQ}=2 \), \( \angle \textrm{POQ} = \frac { \pi } { 4 } \) 이면서 직선 \( \textrm{OP} \)의 아랫부분에 있는 점을 \( \textrm{Q} \).
일단 \( C \)처럼 정의된 수식을 보면 저것은 반원 모양의 그래프라는 것을 바로 떠올릴 수 있어야 합니다.
그리고 점 \( \textrm{P} \), \( \textrm{Q} \)에 대한 설명이 나오는데, 이 상황을 그대로 그림으로 나타내어보면 <그림 1>과 같습니다.
<그림 1>

문제의 그 다음 부분을 읽어보겠습니다.
점 \( \textrm{P} \)가 곡선 \( C \)를 움직이고,
점 \( \textrm{X} \)는 선분 \( \textrm{OP} \) 위를 움직이고,
점 \( \textrm{Y} \)는 선분 \( \textrm{OQ} \) 위를 움직인다.
점 \( \textrm{X} \), \( \textrm{Y} \)에 대한 정의가 새로 나옵니다.
선분 \( \textrm{OP} \), 선분 \( \textrm{OQ} \)는 이미 그림상에 표현해두었으므로,
\( \textrm{X} \), \( \textrm{Y} \)의 위치를 그림상에 표현하는 건 쉽습니다(<그림 2>와 같이).

그리고 벡터 \( \textrm{OZ} \)에 대한 정의가 나옵니다.
$$ \overrightarrow{\textrm{OZ}} = \overrightarrow{\textrm{OP}} + \overrightarrow{\textrm{OX}} + \overrightarrow{\textrm{OY}} $$
벡터 \( \textrm{OZ} \)가 세 벡터의 합으로 정의되어 있습니다.
그런데 여기서 점 \( \textrm{P} \), \( \textrm{X} \), \( \textrm{Y} \)는 모두 어떤 곡선 위를 움직이는 점들이기 때문에
이들을 동시에 생각해서 점 \( \textrm{Z} \)가 나타나는 영역을 찾아주는 것은 생각하기에 무리가 있습니다.
이럴 때는 세 점 중 한 점만을 우선 생각하여 그 한 점이 움직이는 영역을 찾아주고,
그 영역에서 다른 점이 움직이는 것을 고려한 영역을 다시 찾아주는 방식으로
진행해 나가는 것이 생각하기 간편합니다.
이 방식을 이 문제에서는 어떻게 적용할지 구체적으로 살펴보겠습니다.
먼저 점 \( \textrm{P} \)가 움직이는 영역부터 보겠습니다.
점 \( \textrm{P} \)가 움직이는 영역은 이미 나타낸 바가 있습니다(<그림 3>).
<그림 3>

여기에 점 \( \textrm{X} \)가 움직이는 것을 고려하여,
$$ \overrightarrow{\textrm{OP}} + \overrightarrow{\textrm{OX}} $$
가 그리는 영역을 살펴보겠습니다.
벡터 \( \textrm{OX} \)는 벡터 \( \textrm{OP} \)와 같은 방향으로 평행한 벡터이기 때문에,
둘을 더하게 되면 벡터 \( \textrm{OP} \)에 벡터 \( \textrm{OX} \)의 길이만큼이 그대로 연장되는 형태가 됩니다.
이때, 벡터 \( \textrm{OX} \)는 길이를 \( 0 \)부터 \( 2 \sqrt{2} \)까지 가질 수 있습니다.
예를 들어, 점 \( \textrm{P} \)의 \( x \)좌표를 \( 2 \)로 고정시킬 때,
두 벡터의 합은 다음과 <그림 4>와 같은 영역(직선 모양)을 갖게 됩니다.
<그림 4>

이제 점 \( \textrm{Y} \)의 움직임을 고려해보겠습니다.
벡터 \( \textrm{OY} \)는 벡터 \( \textrm{OP} \)로부터 \( 45 ^{\circ} \) 음의 방향으로 회전된,
길이가 \(0 \)에서 \( 2 \)까지 변하는 벡터입니다.
점 \( \textrm{P} \)의 \( x \)좌표를 \( 2 \)로 고정시킬 때, 벡터 \( \textrm{OY} \)는 <그림 5>와 같이 \( x \)축과 평행하게 나타납니다.
<그림 5>

벡터 \( \textrm{OY} \)를 <그림 5>에 표시된 벡터 \( \textrm{OP} \)와 벡터 \( \textrm{OX} \)의 합이 나타내는 영역의 각 점들에 대해
더해주면 <그림 6> 같은 평행사변형 모양의 영역이 나옵니다.
<그림 6>

이제 점 \( \textrm{P} \)의 고정을 풀어서 저 평행사변형이 어떤 새로운 영역을 그리게 되는지
알아보면 되는데, 이것을 바로 생각해내기 조금 어려울 수 있으므로,
점 \( \textrm{P} \)의 \( x \)좌표를 \( 2\sqrt{2} \)로 고정시킨 상태에서 세 벡터 합의 영역을 우선 그려보겠습니다(<그림 7>).
<그림 7>

이렇게 한 다음, 점 \( \textrm{P} \)의 \( x \)좌표가 \( 2 \)에서 \( 2\sqrt{2} \)로 움직일 때, 평행사변형의 각 부분들이
어떻게 움직이고 있는지 확인해봅니다 (<그림 8>).
<그림 8>

평행사변형을 도끼의 날이라고 하고, 선분 \( \textrm{OP} \)를 도끼의 손잡이라고 한다면,
우리가 구하는 영역은 마치 이 도끼를 점 \( \textrm{O} \)를 축으로 \( 45^{\circ} \) 내려찍을 때
도끼의 날이 쓸고 지나가는 영역과 같다고 이해할 수 있습니다.
결국 우리가 구하는 영역은 <그림 9>와 같으며, 이것이 점 \( \textrm{Z} \)가 존재할 수 있는 영역입니다.
문제에서는 이 영역을 \( \textrm{D} \)라고 하였습니다.
또한 영역 \( \textrm{D} \)에 속하는 점 중 \( y \)축과 거리가 최소인 점을 \( \textrm{R} \)이라고 하였으므로,
\( \textrm{R} \)까지 그림에 표시하겠습니다.
<그림 9>

이제 남은 건 점 \( \textrm{R} \)과, 영역 \( \textrm{D} \) 안의 점 \( \textrm{Z} \)에 대해서
$$ \overrightarrow{ \textrm{OR} } \ \cdot\ \overrightarrow{ \textrm{OZ} } $$
의 최댓값과 최솟값을 구하는 것입니다.
이것을 하기 전에 내적 자체에 대해 생각해봅시다.
두 벡터의 내적이란, 두 벡터의 크기를 곱하고, 두 벡터가 이루는 각도의 코사인 값을 곱한 값입니다.
그렇다면 내적이 최대가 되기 위해서는
두 벡터의 크기가 최대한 커야하고, 두 벡터가 이루는 각도의 코사인 값도 최대한 커야합니다.
각도가 \( 0 \) ~ \( 180^{\circ} \)일 때에는 각도가 커질 수록 코사인 값이 작아지기 때문에,
각도의 코사인 값이 최대한 커야 한다는 것의 의미는
두 벡터가 이루는 각도는 최대한 작아야한다는 것이 됩니다.
반대로, 내적이 최소가 되기 위해서는
두 벡터의 크기가 최대한 작아야 하고, 두 벡터가 이루는 각도는 최대한 커야 한다는 것이 됩니다.
이를 염두에 두고 최댓값과 최솟값을 찾아보겠습니다.
먼저 최댓값을 생각해보겠습니다(<그림 10>)
<그림 10>
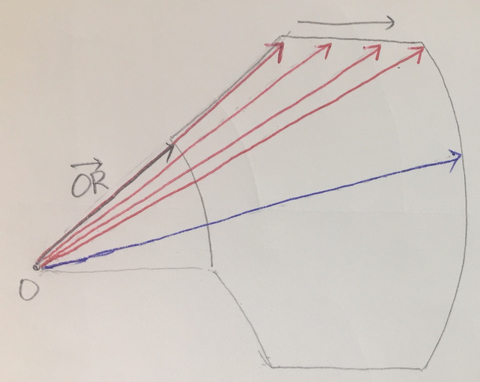
내적이 최댓값이 되도록 하는 벡터 \( \textrm{OZ} \)의 후보는
빨간색, 파란색 벡터와 같은 것으로 생각할 수 있습니다.
그런데 파란색 벡터같은 경우, 빨간색으로 표시한 벡터들 중 가장 오른쪽에 있는 것과 크기는 같으면서
벡터 \( \textrm{OR} \)과 이루는 각도는 더 크므로 고려할 필요가 없습니다.
다만, 빨간 벡터 중에서는, 오른쪽으로 갈 수록 크기는 커지지만
벡터 \( \textrm{OR} \)과의 각도도 같이 커지기 때문에
직관만으로 특정한 어떤 것일 때 내적이 최대다! 라고 단정지으면 조금 위험합니다.
그래서 수식으로 짚고 넘어가는 것이 안전합니다.
내적을 구하는 방법에는 앞에서 설명한
(두 벡터의 크기의 곱) * (두 벡터가 이루는 각도의 코사인 값)
도 있지만,
각 성분의 곱의 합
으로도 계산 가능합니다.
어떤 것이 편한지는 문제마다 달라집니다. 여기서는 각 성분의 곱의 합으로 내적을 계산하겠습니다.
\( \textrm{R} \)과 \( \textrm{Z} \)의 좌표를 <그림 11>과 같이 표시합니다.
<그림 11>

(\( \textrm{Z} \)의 좌표 및 \( x \)의 범위가 왜 그런지는 한번 생각해보시기 바랍니다. 어려운 것은 아닙니다.)
이제 내적을 다음과 같이 계산할 수 있습니다.
$$ \overrightarrow{ \textrm{OR} } \ \cdot\ \overrightarrow{ \textrm{OZ} } = (2, \ 2) \ \cdot \ (4+x, \ 4) $$
$$ \qquad\qquad =(8 + 2x) + 2 \cdot 4 $$
$$ \qquad =16+2x. $$
\( x \)의 범위는 \( 0 \) 이상 \( 2 \) 이하이므로, 내적의 최댓값은 \( 20 \)이 됩니다.
그리고 최솟값에 대해서도 생각해봅시다(<그림 12>).
<그림 12>

그림에 표시된 빨간색 벡터와 파란색 벡터 각각의 역할은
최댓값을 생각할 때와 비슷하게 생각하면 됩니다.
이 경우에서도 역시 \( \textrm{Z} \)의 좌표 및 \( x \)의 범위가 왜 이렇게 되는지 생각해보세요.
내적을 구하면,
$$ \overrightarrow{ \textrm{OR} } \ \cdot\ \overrightarrow{ \textrm{OZ} } = (2, \ 2) \ \cdot \ (2\sqrt{2}+x, \ -x)$$
$$ = 4\sqrt{2}. \qquad $$
계산 과정에서 \( x \)가 소거되어버리므로, \( x \)의 범위에 관계없이 값은 \( 4\sqrt{2} \)이며, 이것이 최솟값입니다.
결국 벡터 \( \textrm{OR} \)과 벡터 \( \textrm{OZ} \)의 내적의 최댓값과 최솟값의 합은
$$ 20 + 4\sqrt{2} $$
이므로, 최종적으로 구하는 값
$$ a + b = 24 $$
가 되어, 정답은 \( 24 \)입니다.
벡터와 관련된 고난도 문제는 이 문제의 \( \textrm{P} \), \( \textrm{X} \), \( \textrm{Y} \)와 같이 여러 점이 변수가 되어
다변수함수적인 해석, 즉 고등학교 과정을 벗어나는 내용을 필요로 하는 것이 아닌가 하는
당황스러움을 줄 수도 있습니다.
하지만 하나씩 풀어서 생각해보면 그런 게 필요없다는 것을 곧 알아차릴 수 있으며,
우리가 생각 가능한 범위 내로 문제를 끌어와서 해결할 수 있습니다.
이상으로 2020학년도 6월 고3 평가원 모의고사 수학 가형 30번 문제의 풀이를 모두 마치겠습니다.
'수능수학 > 2020 수학가형' 카테고리의 다른 글
| [4점공략] 2020 6월 고3 평가원 모의고사 수학 가형 30번 (1) | 2019.06.19 |
|---|---|
| [4점공략] 2020 6월 고3 평가원 모의고사 수학 가형 21번 (0) | 2019.06.19 |


