| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- LineRenderer
- 딥러닝
- xcode
- 유니티
- 포랩
- JavaScript
- Unity
- 모의고사
- 1등급사과
- 과탐
- 수능
- 생명과학1
- 바른생수
- MNIST
- 수학가형21번
- customdialog
- 내신
- 생명과학
- 개발
- kotlin
- PoLAB
- 코틀린
- ios
- 고등학생
- Android
- 플레이스토어
- Firebase
- 고등학교
- 수학가형
- 개발일지
- Today
- Total
수학적 접근
[4점공략] 2017 수능 수학 가형 29번 본문

2017 수능 수학 가형 29번의 문제입니다.
항상 29번은 평면도형에서의 삼각함수 공식을 이용한 문제 해결 또는 공간도형/공간좌표/벡터 문제가 나오는 것으로
거의 정형화되어있다시피 합니다.
이번에는 공간도형, 벡터 쪽의 문제가 출제되었습니다.
사실 삼각함수 공식이 덧셈정리만 남기고 교육과정에서 제외되어 이제 29번 문항이 공간도형, 벡터 쪽으로
자리잡았다고 생각할 수도 있겠지만, 제외된 모든 삼각함수 공식들은 덧셈정리로부터 유도되는 공식이기 때문에
꼭 그렇다고 단정지을 수는 없을 듯합니다.
삼각함수 단원의 문제 출제 양상이 어떻게 달라질지는 두고보아야 할 일인 것 같습니다.
이 문제는 겉모습은 벡터 문제의 모양을 띠고 있으나 문제 자체는 공간도형에 대한 문제이며,
실질적으로 문제를 풀어나가는 데 있어 공간도형의 성질만 이용하여도 풀어나갈 수 있는 문제입니다.
이 문제는 풀어나갈 때 유별난 아이디어를 요구하지 않기 때문에, 평소에 공간도형에 대한 공부를 착실히 했다면
그리 어렵지 않게 풀어나갈 수 있었을 것입니다.
문제 풀이에 들어가보도록 하겠습니다.
*직접 노트에 그림을 그려가며 따라오는 것이 풀이 이해에 더 도움이 될 것입니다.
이 문제는 모의고사, 수능에서 주로 사용하는 방법으로, 난도를 높이는 방법 중 하나가 적용되었습니다. 바로 '그림 안 주기'입니다.
다르게 해석될 여지가 없는 문장만으로 도형들을 묘사만 해놓는 방식입니다.
문제를 읽어나가면서 도형을 정확히 구성해야하기 때문에 시간을 잡아먹는 요소가 된다는 점에서 부담을 느끼게 하는 것이지요.
문제를 정확히 읽어서 아래와 같이 도형, 보조선, 수치를 나타냅니다.
(여기서 한 가지 말씀드리고 싶은 것은, 시험지 위에 그림을 그릴 때는 크게크게 그리라는 것입니다.
조그맣게 그려놓고 하다보면, 각종 보조선 및 수치가 붙어나가면서 자기가 뭘 나타낸 것인지 혼동이 올 수 있습니다.
그림을 그릴 때는 크게 크게 시원하게!)

삼각형 \( \rm{ABC} \)의 무게중심을 \( \rm{O} \)라 하고, 점 \( \rm{A} \)에서 선분 \( \rm{BC} \)에 내린 수선의 발을 \( \rm{H} \)라 합니다.
정사면체의 한 모서리의 길이가 \( 4 \)이므로, 정사면체를 이루는 한 삼각형의 높이

입니다.
점 \( \rm{O} \)는 이를 \( 2:1 \)로 내분하므로, 그림과 같은 길이 구성을 가집니다.
또한, 정사면체의 성질에 의해, 점 \( \rm{D} \)에서 삼각형 \( \rm{ABC} \)에 내린 수선의 발은 삼각형 \( \rm{ABC} \)의 무게중심, 즉 \( \rm{O} \)입니다.
따라서 그림과 같이 선분 \( \rm{AH} \)와 선분 \( \rm{DO} \)는 수직이라는 것을 알 수 있습니다.
뒤이어나오는 \( \rm{Q} \)에 대한 묘사를 계속 읽어나가면서 그림을 완성합니다.
점 \( \rm{Q} \)는 삼각형 \( \rm{BCD} \) 위에 있으면서, 벡터 \( \rm{OQ} \)가 벡터 \( \rm{OP} \)에 수직이 되도록 하는 점이라고 되어 있습니다.
여기서 우리는 점 \( \rm{Q} \)가 삼각형 \( \rm{BCD} \)에서 어떤 위치에 있을 수 있는지를 파악해야합니다.
우선 가장 생각하기 쉬운 것은, 선분 \( \rm{DH} \) 위에서 그러한 \( \rm{Q} \)를 찾는 것입니다.
그러한 \( \rm{Q} \)를 \( \rm{Q'} \)으로 두겠습니다.

벡터 \( \rm{OP} \)에 수직이 되도록 하고 점 \( \rm{O} \)를 지나는 모든 직선들을 모은다면, 그것은 선분 \( \rm{OQ'} \)을 포함하고, 벡터 \( \rm{OP} \)에 수직인 평면입니다.
그리고 삼각형 \( \rm{BCD} \)를 포함하는 평면을 생각한다면, 앞에서 언급한 두 평면의 교선은 반드시 직선입니다.
이때, 이 교선 중 삼각형 \( \rm{BCD} \)의 내부에 있는 선분만 생각한다면,
이 선분은 선분 \( \rm{BC} \)에 평행하도록 나타나면서, 점 \( \rm{Q'} \)을 지나는 선분이 될 것입니다.

(사진에 잘못 기재된 부분: 사진에 선분 \( \rm{PQ} \)라고 작성된 부분을, 선분 \( \rm{OP} \)로 바꾸어서 생각해주세요)
점 \( \rm{Q} \)의 자취를 찾았습니다. 이러한 \( \rm{Q} \)들 중,

, 즉 선분 \( \rm{PQ} \)의 길이가 최대가 되도록 하는 \( \rm{Q} \)의 위치를 찾으면 됩니다.
위의 그림에서 그러한 점을 찾기는 쉽습니다. 파란색 선분의 가장 끝점일 것입니다.
아래 그림에서 빨간색으로 나타낸 선분의 길이가 우리가 구하는 값이 됩니다.

(사진에 잘못 기재된 부분: 사진에 선분 \( \rm{PQ} \)라고 작성된 부분을, 선분 \( \rm{OP} \)로 바꾸어서 생각해주세요)
이를 구하기 위해 차근차근 단계를 밟아나갑니다.
정사면체 전체의 그림 중 삼각형 \( \rm{DAH} \)를 떼어 가져와서 분석을 시작합니다.
이 삼각형에서의 우리의 목적은 선분 \( \rm{HQ'} \)의 길이를 알아내는 것입니다.
그럴 수 있다면, \( \rm{OQ} \)가 최댓값이 나오도록 하는 \( \rm{Q} \)점의 값을 \( \rm{Q_M} \)라 했을 때,
\( \rm{CQ_M} \)의 값을 파악할 수 있으며, 여기서 \( \rm{DQ_M} \)을 알게 되어, 결과적으로
\( \rm{PQ_M} \)을 구할 수 있기 때문입니다.

그림에 표시된 각 \( \alpha, \ \theta \) 에 대한 것(

) 은 정사면체의 성질에서 이끌어낼 수 있습니다.
이 부분은 암기하고 있는 것이 편하지만, 정사면체 상에서 쉽게 유도해낼 수 있습니다.
\( \rm{P} \)에서 선분 \( \rm{AH} \)에 내린 수선의 발 \( \rm{H_2} \)를 생각했을 때, 위에서 구한 각 \( \alpha \)의 코사인값을 이용하면,

이며, \( \rm{H_2} \)가 선분 \( \rm{AO} \)를 이등분한다는 것이 나오게 되므로,
삼각형 \( \rm{PAO} \)가 이등변삼각형인 것이 나오게 됩니다.
따라서, 선분 \( \rm{OP} \)의 길이는 \( 2 \)가 됩니다.

더 자세한 분석을 위해 사각형 \( \rm{PH_2HQ'} \)을 떼어옵니다.

위 그림에서 삼각형 \( \rm{H_2PO} \)와 삼각형 \( \rm{H_3OQ'} \)가 닮음임을 알 수 있습니다.

라 했을 때, 알고 있던 단서를 이용하여 각 선분의 길이를 \( a \)를 이용하여 나타낼 수 있습니다.
여기서 닮음이라는 단서를 이용하여 \( a \)의 값을 알아낼 수 있습니다.
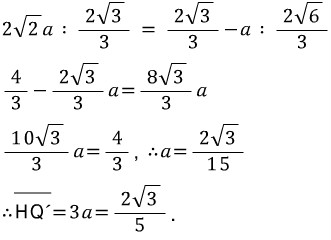
\( \overline{\rm{HQ'}} \)의 값을 알게 되었으므로, 앞에서 했던 논의에 맞추어서 답을 구하는 과정까지 가보겠습니다.
삼각형 \( \rm{BCD} \)를 떼어서 가져옵니다.
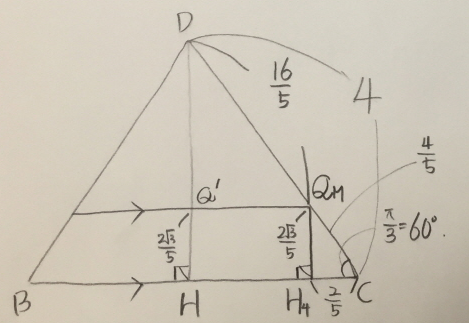
위 그림에서 삼각형

를 보았을 때,

이므로,
이는 우리가 흔히 보아오던 1:루트3:2의 비를 가지는 삼각형입니다.
따라서

이며,

임이 손쉽게 구해집니다.
마지막으로, 삼각형 \( \rm{DPQ_M} \)을 떼어옵니다.

위에서 코사인 법칙을 적용할 수도 있겠지만, 코사인 법칙은 교육과정에서 제외된 항목이므로,
피타고라스 정리의 반복 적용을 통해,

임을 구해냅니다.
따라서, \( p=5, \ q=14 \)가 되어, 최종적으로 구하는 값 \( p+q=19 \)입니다.
이상으로 2017학년도 수능 수학 가형 29번의 문제 풀이를 마치도록 하겠습니다.
'수능수학 > 2017 수학가형' 카테고리의 다른 글
| [4점공략] 2017 수능 수학 가형 30번 (0) | 2019.06.30 |
|---|---|
| [4점공략] 2017 수능 수학 가형 21번 (0) | 2019.06.30 |


