| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- xcode
- 고등학교
- MNIST
- customdialog
- Android
- Unity
- kotlin
- 유니티
- 수학가형21번
- 과탐
- 수학가형
- 내신
- 코틀린
- 생명과학1
- 1등급사과
- 개발
- 플레이스토어
- LineRenderer
- 수능
- Firebase
- 딥러닝
- PoLAB
- 개발일지
- JavaScript
- 모의고사
- 포랩
- 고등학생
- 바른생수
- 생명과학
- ios
- Today
- Total
수학적 접근
[4점공략] 2017 수능 수학 가형 21번 본문

언제나 당당하게 객관식의 마지막 21번 자리를 지키는 미적분 문항입니다..!
이번 수능 수학 수리 가형 21번 문항의 총평을 하자면, 정적분과 부정적분을 모두 아우르는 포괄적인 문제였다는 점을 말하고 싶습니다.
정적분이 가지는 의미와 부정적분이 가지는 의미는, 같은 점도 있지만, 둘은 확실히 다릅니다.
부정적분은 '어떤 함수를 미분하여야 이 함수(피적분함수)가 되는가' 하는,철저히 함수의 측면에서 바라보아야 합니다.
반면, 정적분은, '넓이'로 정의되어 있습니다.
정적분 과정에서 부정적분을 구하여 위끝과 아래끝을 대입하는 것은,
정적분의 여러 성질 중 어떤 정리 하나를 이용하는 것에 지나지 않습니다.
이 문제는 정적분의 넓이라는 개념을 이용하여 그림을 이용하고,
또 부정적분을 해결하기 위한 함수라는 도구 또한 이용하여야 풀 수 있었던 문제입니다.
한 문항으로 여러 개념을 물어보는 점에서는 수능스러운 문제였으나, 난도 자체는 그리 높지 않았습니다.
앞에서 설명한 기본적인 개념만 잘 갖춰져 있다면, 이 문제를 풀어나가는 아이디어를 생각해내는 데 별 어려움을 느끼지 않았을 것이며,
풀어나가는 과정도 어렵게 느끼지 않았을 것이라고 생각합니다.
그럼 풀이를 살펴보도록 하겠습니다.
문제를 읽어나갑니다.
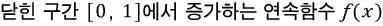
이 문장에서 가장 유심히 보아야 할 것은 '증가함수'라는 조건입니다.
함수에 있어서 꽤 강력한 조건이지요.
그리고 연속함수라는 표현이 있으니, 주어진 구간에서 적분가능하도록 하는 조건이 주어졌구나 하는 점도 대략 생각할 수 있습니다.
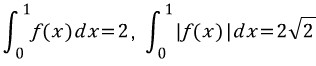
여기서는, 동일한 구간에서, 같은 함수를 그냥 적분한 것과, 절댓값을 씌운 것의 정적분 값이 다름을 알 수 있습니다.
당연히 절댓값을 씌운 것의 정적분 값이 더 큽니다.
이렇게 나올 수 있으려면, 함수 f(x)는 주어진 구간에서 음의 값을 가지는 상태가 존재해야합니다.
그리고, 앞에서 살펴본 '증가함수'라는 조건에 맞춰보았을 때,
함수 f(x)는 대략 다음과 같은 모양인 것으로 생각할 수 있습니다.
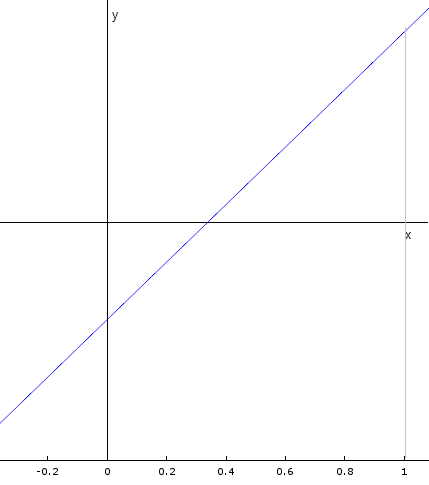
물론 직선인지 곡선인지는 알지 못하지만, 그래프가 증가를 하며,
음의 값을 가지는 구간이 존재한다는 것을 표시해주면 위와 같은 그림을 얻을 수 있습니다.
그리고 반드시 구간 내에서 반드시 x축과의 교점이 생긴다는 것도 알 수 있습니다.
** \( x \)축과의 교점은 하나가 아닐 수도 있습니다. 함수 f(x)가 x축 위로 어떤 길이를 가지도록 지날 수도 있습니다.
우리가 배워 온 로그, 다항, 삼각, 지수함수들을 마구 섞어놓아도 그런 그래프는 그려질 수 없지만,
f(x)는 그런 함수라고 보장되지는 않지요.
x축과의 교점을 a라고 두고, x축 아래, x축 위로 생긴 넓이들을 각각
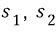
로 둡니다.
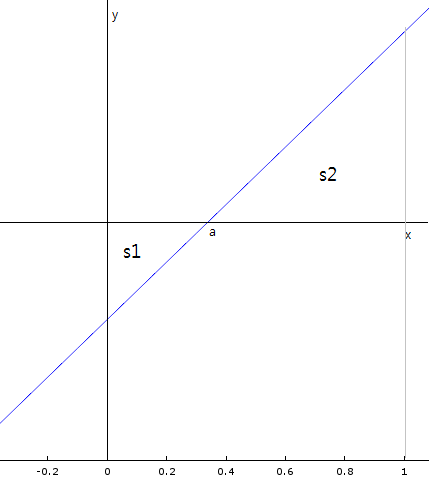
위의 **에서 말한 부분은 계속 유심히 지켜보아야 할 사항입니다.
a라는 점이 **에서 말한 상황에서는 어떻게 결정되어야 할까를 생각합니다.
**에서 말한 상황에서는, 무한히 많은 a의 값 중 임의로 하나를 선택하는 형태로 생각할 수 있습니다.
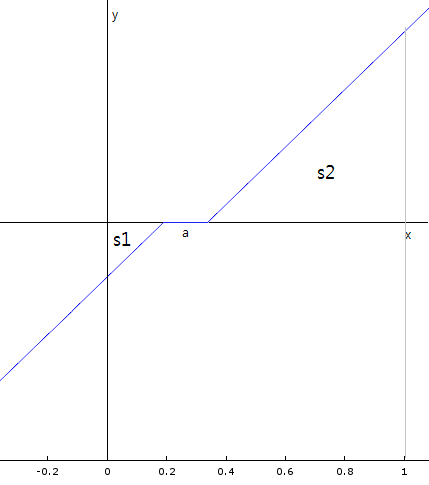
a가 x축 위에 놓인 그래프의 어디에 위치하든, s1과 s2의 넓이는 변하지 않습니다.
즉, 그래프가 이것처럼 생겼든, 앞의 것처럼 생겼든 관계가 없습니다.
여기서, 문제에서 주어진 조건을 이용하여 s1과 s2를 구할 수 있습니다.
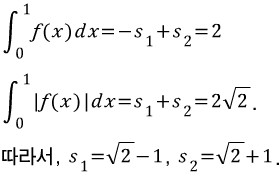
정적분의 넓이 개념을 이용하여 구해냅니다.
이제 문제의 나머지 부분을 읽어서 답을 구하는 과정까지 가보도록 하겠습니다.
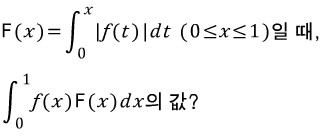
F(x)로 주어져있는 식은, 피적분함수에 절댓값이 없었더라면 아주 익숙하게 보아왔던 식입니다.
그리고 우리는 절댓값을 없앨 수 있는 방법을 알고 있습니다.
앞에서 정한 x=a 지점 이전과 이후로 나누는 것입니다.
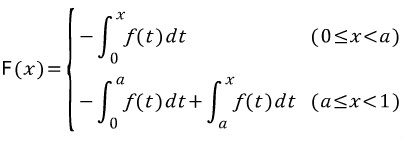
(a를 기준으로 한 등호 붙임은, 어디로 붙이든 관계없습니다)
그리고 이 익숙해진 형태에 익숙하게 적용해왔던 방법을 적용합니다(양변을 미분).
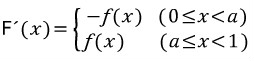
이쯤 되면, 마지막으로 구하게 되는 값인
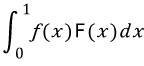
의 값을 어떻게 구해야할지 감이 잡힙니다.
x=a를 기준으로 나누어서, 각각 치환적분을 이용하게 될 듯합니다.
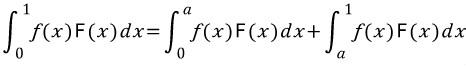

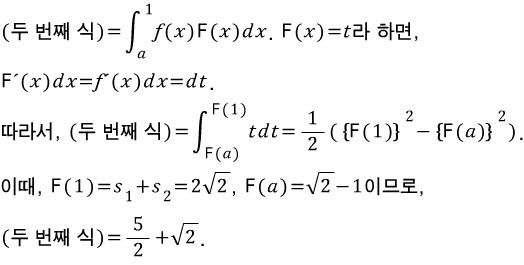

이상으로 2017학년도 수능 수학 가형 21번 풀이를 마치도록 하겠습니다.
대학 입시 고민, 모르는 과학 문제, 서울대학교 사범대 출신 선생님의 풍부한 공/사교육 경험으로 해결해드립니다. (현재 무료!)
'포랩(PoLAB)' - 입시 질문, 과학 공부 질문, 여기에 물어보세요!
과학 공부하다가 모르는 것이 생겼는데 마땅히 질문할 곳이 없다면, 각종 복잡한 수시 전형, 정시 전략에 머리가 아픈데 속시원히 마음 잡아줄 사람이 없다면, 바로 여기에서 도움을 드릴 수 있
dkfk2747.tistory.com
'수능수학 > 2017 수학가형' 카테고리의 다른 글
| [4점공략] 2017 수능 수학 가형 30번 (0) | 2019.06.30 |
|---|---|
| [4점공략] 2017 수능 수학 가형 29번 (0) | 2019.06.30 |


